Detect cycle in Directed graph

Given a directed graph, chech whether the graph contain a cycle or not. Your method should return true if the given graph have atleast one cycle, else return false. For example the following graph have 3 cycle 2 -> 0 ->2, 2 -> 0-> 1 ->2, and 3 -> 3. so your method must return true. Depth first Search(DFS) of a tree can be used to detect a cycle in a Graph. If DFS is applied over a directed and connected graph, it gives a tree. If tree contains a back edge, we can say graph has a cycle.

Back edge in a Graph

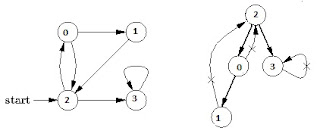Consider an edge (u,v) is said to be a back edge, if node 'v' is an ancestor of node 'u' in a tree when DFS applied. Basically, a back edge is an edge which is from a node to itself(self loop) or to an ancestor. In the given graph, there are 3 back edges, marked with cross sign. We can observe that 3 back edges indicate that 3 cycle present in a graph.

Java program to detect cycle in directed graph

To detect a cycle in a directed graph, we need to detect back edge. We will store the vertices in recursion stack of DFS traversal. If we reach a vertex that is already in the recursion stack, then there is a cycle in the tree. The edge that connects current vertex to the vertex in the recursion stack is back edge. We have used recStack[] array to keep track of vertices in the recursion stack.

package com.walking.techie.data.structure.graph;

import java.util.Iterator;
import java.util.LinkedList;

//java program to detect cycle in directed graph
public class DetectCycleInDirectedGraph {

  private int v; // no of vertices in a graph
  private LinkedList<Integer> adj[];// array of linked list if adjacency list
  // representation

  public DetectCycleInDirectedGraph(int v) {
    this.v = v;
    adj = new LinkedList[v];
    for (int i = 0; i < v; i++) {
      adj[i] = new LinkedList<Integer>();
    }
  }

  public static void main(String[] args) {
    DetectCycleInDirectedGraph g = new DetectCycleInDirectedGraph(4);

    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 2);
    g.addEdge(2, 0);
    g.addEdge(2, 3);
    g.addEdge(3, 3);

    if (g.isCyclic()) {
      System.out.println("Graph contain cycle.");
    } else {
      System.out.println("Graph doesn't contain cycle.");
    }
  }

  // addEdge method to add edge between vertex i and vertex j
  public void addEdge(int i, int j) {
    adj[i].add(j);
  }

  public boolean isCyclic() {
    // mark all the vertices not visited
    boolean visited[] = new boolean[this.v];
    boolean recStack[] = new boolean[this.v];
    for (int i = 0; i < this.v; i++) {
      if (isCyclicUtil(i, visited, recStack)) {
        return true;
      }
    }
    return false;
  }

  private boolean isCyclicUtil(int i, boolean[] visited, boolean[] recStack) {
    //mark current node as visited and part of recursion stack
    visited[i] = true;
    recStack[i] = true;
    Iterator<Integer> itr = adj[i].iterator();
    while (itr.hasNext()) {
      int n = itr.next();
      if (!visited[n] && isCyclicUtil(n, visited, recStack)) {
        return true;
      } else if (recStack[n]) {
        return true;
      }
    }
    recStack[i] = false; // remove the vertex from recursion stack
    return false;
  }
}

Output of above program is shown below:

Graph contain cycle.

Note : This code has been compiled and run on mac notebook and intellij IDEA.

find the above working code from git.