Depth First Traversal of a Graph

Traversal of the graph is used to perform task such as searching for certain node. The graph may contain cycles, so we may come to same node again while traversing. To avoid it, we need to keep track of visited node, so we can not come again to the same node, we use a boolean visited array.

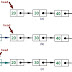
Lets understand it with example. In the following graph, we start traversing from vertex 0 when we come to vertex 1, we look for all adjacent vertices of it. 0 is also adjacent of vertex 1. if we don't mark visited vertex, we again process the vertex 0 and it will go into non-terminating loop. A depth first search of following graph is 0, 1, 2,3.

Following is the java implementation of depth first traversal of a graph. It uses adjacency list representation of graphs.

import java.util.Iterator;
import java.util.LinkedList;

//java program to print DFS traversal of given graph
public class DepthFirstTraversal {
 private int v; // no of vertices in a graph
 private LinkedList<Integer> adj[];// array of linked list if adjacency list
              // representation

 public DepthFirstTraversal(int v) {
  this.v = v;
  adj = new LinkedList[v];
  for (int i = 0; i < v; i++) {
   adj[i] = new LinkedList<Integer>();
  }
 }

 // addEdge method to add edge between vertex i and vertex j
 public void addEdge(int i, int j) {
  adj[i].add(j);
 }

 public void DFS(int s) {
  // mark all the vertices not visited
  boolean visited[] = new boolean[this.v];
  // call the recursive method to print DFS traversal
  DFSUtil(s, visited);
 }

 public void DFSUtil(int s, boolean[] visited) {
  // mark the current vertex as visited and print it
  visited[s] = true;
  System.out.print(s + " ");
  // recur all the vertices adjacent to this current vertices s
  Iterator<Integer> itr = adj[s].iterator();
  while (itr.hasNext()) {
   int n = itr.next();
   if (!visited[n])
    DFSUtil(n, visited);
  }
 }

 public static void main(String[] args) {
  DepthFirstTraversal g = new DepthFirstTraversal(5);
  g.addEdge(0, 1);
  g.addEdge(0, 2);
  g.addEdge(1, 0);
  g.addEdge(1, 2);
  g.addEdge(1, 3);
  g.addEdge(3, 3);

  System.out.println("Following is Depth First Traversal "
                                  + "(starting from vertex 0)");

  g.DFS(0);
 }
}

In the above code traverse only the vertices that are reachable from the given vertex. It will not work for the graph that is disconnected graph or vertices are not reachable from the given source vertex. To do complete depth first traversal of a graph we need to modify the code. We need to call DFSUtil() method for every vertices and before calling the DFSUttil() method, we should check if it is already printed or visited by other call of DFSUtil() method. Following implementation does the complete graph traversal even if the nodes are unreachable or disconnected.

You can consider the below disconnected directed graph.

import java.util.Iterator;
import java.util.LinkedList;

//java program to print DFS traversal of given graph
public class DepthFirstTraversal {
 private int v; // no of vertices in a graph
 private LinkedList<Integer> adj[];// array of linked list if adjacency list
          // representation

 public DepthFirstTraversal(int v) {
  this.v = v;
  adj = new LinkedList[v];
  for (int i = 0; i < v; i++) {
   adj[i] = new LinkedList<Integer>();
  }
 }

 // addEdge method to add edge between vertex i and vertex j
 public void addEdge(int i, int j) {
  adj[i].add(j);
 }

 public void DFS() {
  // mark all the vertices not visited
  boolean visited[] = new boolean[this.v];
  // call the recursive method to print DFS traversal
  for (int i = 0; i < this.v; i++) {
   if (visited[i] == false)
    DFSUtil(i, visited);
  }

 }

 public void DFSUtil(int s, boolean[] visited) {
  // mark the current vertex as visited and print it
  visited[s] = true;
  System.out.print(s + " ");
  // recur all the vertices adjacent to this current vertices s
  Iterator<Integer> itr = adj[s].iterator();
  while (itr.hasNext()) {
   int n = itr.next();
   if (!visited[n])
    DFSUtil(n, visited);
  }
 }

 public static void main(String[] args) {
  DepthFirstTraversal g = new DepthFirstTraversal(5);
  g.addEdge(0, 1);
  g.addEdge(0, 2);
  g.addEdge(1, 0);
  g.addEdge(1, 2);
  g.addEdge(3, 3);
  g.addEdge(2, 4);

  System.out.println("Following is Depth First Traversal ");

  g.DFS();
 }
}

Output of above program is shown below:

Following is Depth First Traversal
0 1 2 4 3

Time Complexity: O(V+E) where V is number of vertices in the graph and E is number of edges in the graph.